Crazy Witch Game
One of my earlier attempts at using my computer to solve puzzles was “The Crazy Witch Game” from 1996. I was given this game as a gift, along with a very similar “Crazy Frog Game”.

According to the box the game came in, it was designed by Ari Ron and made by Shafir Games of Israel in 1981. Unfortunately I can’t find any references to it on the internet, although Shafir Games still appear to exist.

The object of the game is to arrange the nine cards in a square in such a way that heads and tails of the same colour match. The picture below illustrates a matching head and tail.

According to the box there are two possible solutions. We shall see about that!
I decided that I would attempt to solve the puzzle by brute force. In other words, by trying out each piece in turn in every possible combination until I’d tried all possible combinations. A quick calculation suggests that this could take some time:
There is a precise upper bound on the number of possible configurations of the pieces one needs to consider in order to find all of the solutions. Each of the nine pieces can appear in one of four orientations in one of nine positions. This gives us (94)(84) … * (1*4) possible layouts of the grid, better written as 9! * 4^9, which equals 95,126,814,720. A big number!
To reduce the number of possibilities I needed to consider, the code performs a depth first search. Very simply, the code tries pieces in turn until it either finds a solution or else runs out of pieces that will fit. If it finds a solution it makes note of it, then carries on. If it runs out of pieces, it goes back to the last point where it had a choice of which piece to try out and tries the next possible choice instead.
Luckily we know in advance that this puzzle can have a maximum depth of 36. That’s nine pieces in the four possible orientations. This gave me an interesting idea for a solution. Rather than write a complicated piece of search code using tree structures and recursion, how about putting everything in a single routine of nested attempts to fit pieces?
Naturally, this is not a recommended approach for most tasks. In fact it did cause a few development headaches and stretched the compiler to its limits (and beyond.) The code contains a lot of repetition, thoroughly contravening the Pragmatic Programmer’s DRY - Don’t Repeat Yourself maxim. As it stands, the software is a definite candidate for refactoring. It works, but I wouldn’t want to maintain it.
On a modern PC the final code evaluates and discovers all possible solutions in under a second.
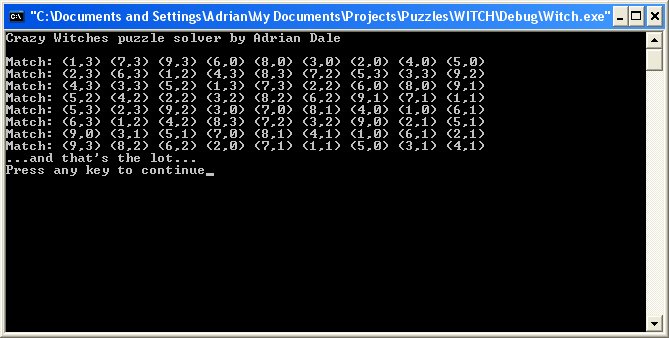
You’ll notice that the code claims to have found eight results. Closer inspection shows that there are only two unique solutions but with four possible rotations of the puzzle for each.
Final Musings
I shelved this project once I’d achieved the results I was looking for. It wasn’t something I had ever planned to maintain. However, there could still be some scope for further exploration of this particular puzzle.
For example, Why did the puzzle have two solutions? Is it possible to make one with a unique solution? Writing a program to find out the answer could be a significant challenge.
Also, can the method of solution be generalised to other puzzle types?




